Σε αυτό το άρθρο, θα ρίξουμε μια ματιά σε μια ενδιαφέρουσα στρατηγική γνωστή ως στοίχημα αξίας. Είναι πιο περίπλοκο από το σίγουρο στοίχημα και έχει μεγαλύτερο κίνδυνο, αλλά προσφέρει επίσης ορισμένα πλεονεκτήματα.
Ας ρίξουμε μια ματιά στην "κουζίνα" των εταιρειών στοιχημάτων.
Φανταστείτε ένα κέρμα, ένα συνηθισμένο κέρμα με δύο πλευρές: κορώνα και γράμματα. Υποθέστε ότι κάποιος ποντάρει ότι μπορεί να μαντέψει την ανώτερη πλευρά του αναποδογυρισμένου νομίσματος. Είναι προφανές ότι η πιθανότητα να πέσει το κέρμα σε οποιαδήποτε από τις πλευρές του είναι 50/50. Έτσι, θα ήταν δίκαιο να ορίσουμε απόδοση 2 για κορώνα και 2 για γράμματα. Αυτό σημαίνει ότι αν δύο παίκτες κάνουν ένα ποντάρισμα και βάλουν από ένα δολάριο σε διαφορετικά αποτελέσματα, ο νικητής θα πάρει 2 δολάρια και ο χαμένος δεν θα πάρει τίποτα.
Ωστόσο, οι εταιρείες στοιχημάτων δεν το κάνουν ποτέ αυτό. Στην καλύτερη περίπτωση, ένας εταιρεία στοιχημάτων θα βάλει απόδοση 1,9 για κορώνα και 1,9 για γράμματα. Αν οι παίκτες μας τοποθετήσουν τα πονταρίσματά τους μέσω μιας εταιρείας στοιχημάτων και επίσης στοιχηματίσουν 1 δολάριο ο καθένας, ο νικητής θα πάρει μόνο 1,90 δολάρια, καθώς 0,10 δολάρια θα καταβληθεί ως προμήθεια του εταιρεία στοιχημάτων. Αυτό ονομάζεται περιθώριο. Και έτσι οι εταιρεία στοιχημάτων βγάζουν το ψωμί τους.
Έτσι, σε έναν ιδανικό κόσμο και σε μια κατάσταση όπου μια εταιρεία στοιχημάτων θα πληρώσει όλα τα χρήματα των πονταρισμάτων ως βραβείο, η απόδοση των εκδηλώσεων θα έπρεπε να σχετίζονται με κάποιον τρόπο:
1/K1 + 1/K2 + … + 1/Kn = 1
Εδώ K1, K2, … Kn είναι η απόδοση για κάθε έναν από τους n αντίθετους εκβάσεις εκδήλωσης – για παράδειγμα, πονταρίσματα 1, X, 2. Καθεμία από την απόδοση πρέπει να είναι ίση με 1 διαιρεμένο με την πιθανότητα ενός αντίστοιχου αποτελέσματος.
Ωστόσο, αν πάρουμε μια πραγματική γραμμή από οποιονδήποτε εταιρεία στοιχημάτων και υπολογίσουμε το άθροισμα των πιθανοτήτων, αυτό δεν θα είναι ίσο με 1. Ας χρησιμοποιήσουμε την απόδοση της Bwin για έναν αγώνα της Ίντερ με την Πόρτο ως παράδειγμα.
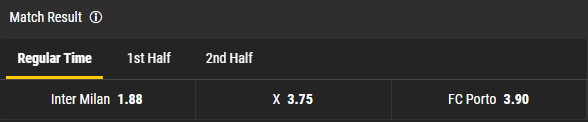
1/1.88 + 1/3.75 + 1/3.90 = 1,054 ( > 1 !!! )
(1,054 - 1) * 100% = 5,4% περιθώριο
Επομένως, η απόδοση στοιχημάτων πάντα θέτουν τις αποδόσεις τους με τρόπο που τους δίνει πλεονέκτημα έναντι των παικτών. Μειώνουν την απόδοση, υπολογίζοντας τα έσοδά τους. Η πιθανότητα είναι με το μέρος του εταιρεία στοιχημάτων. Γι' αυτό το λόγο, η πλειοψηφία (περίπου 98%) των συνηθισμένων παικτών, που ποντάρουν "για τύχη", χάνουν όλα τους τα χρήματα μακροπρόθεσμα.
Όπως μπορείτε να δείτε από την περιγραφή του περιθωρίου, κάθε εταιρεία στοιχημάτων προσπαθεί να μαντέψει την πιθανότητα αυτού ή εκείνου του αποτελέσματος και να ορίζει χαμηλή απόδοση γι' αυτό. Ωστόσο, συμβαίνει ότι οι εταιρείες στοιχημάτων κάνουν λάθη και ορίζει υψηλή απόδοση αντ' αυτού.
Γυρνώντας πίσω στο παράδειγμα του ρίχνοντας το κέρμα, ας υποθέσουμε ότι μια εταιρεία στοιχημάτων αποφάσισε ότι η κορώνα είναι πιο πιθανό να εμφανιστεί και έθεσε απόδοση 2,1 για κορώνα και 1,75 για γράμματα. Προφανώς, ο εταιρεία στοιχημάτων κάνει λάθος. Εάν ένας παίκτης γνωρίζει ότι η πιθανότητα και των δύο αποτελεσμάτων είναι ακριβώς 50%, θα είναι πολύ καλύτερα να στοιχηματίσει σε κεφάλι.
Εάν ο παίκτης τοποθετήσει 100 στοιχήματα σαν αυτό, ποντάροντας ένα δολάριο κάθε φορά, θα κερδίσει με πιθανότητα 50%. Ως εκ τούτου, ο παίκτης θα κερδίσει 100 х 50% х 2.1 = 105 δολάρια. Με έναν επαρκώς μεγάλο αριθμό στοίχημα αξίας, ο παίκτης θα έχει κέρδος 5%. Δεδομένου ότι ο νόμος της πιθανότητας είναι με το μέρος του παίκτη σε αυτή την περίπτωση, η τράπεζά του θα αυξηθεί μακροπρόθεσμα.
Για να εξηγήσουμε αυτή την ιδέα, ας χρησιμοποιήσουμε ένα άλλο παράδειγμα, αυτή τη φορά με μια ζαριά. Είναι προφανές ότι η πιθανότητα να εμφανιστεί οποιοσδήποτε αριθμός είναι 1 στις 6. Ας χρησιμοποιήσουν δύο παίκτες τους ακόλουθους κανόνες: ο πρώτος σκέφτεται έναν αριθμό και ρίχνει τη ζαριά. Εάν κερδίσει, θα πάρει 5 δολάρια από τον άλλο. Εάν χάσει, δίνει στον άλλον ένα δολάριο. Είναι σαφές ότι ο πρώτος παίκτης δεν θα έχει τίποτα (εκτός από μια τρύπα στη τσέπη) πολύ σύντομα. Ας αλλάξουμε τους κανόνες: αν ο πρώτος παίκτης μαντέψει τον αριθμό, θα πάρει 7 δολάρια. Αν δεν το κάνει, θα δώσει ένα δολάριο. Τώρα, ο πρώτος παίκτης θα χρεοκοπήσει τον δεύτερο σε χρόνο μηδέν.
Ένα <0>στοίχημα αξίας είναι ένα στοίχημα που καθιστά την παρακάτω ανίσχυρη αληθινή:
K * P > 1
όπου K είναι η απόδοση και P είναι η πραγματική πιθανότητα αυτού του αποτελέσματος.
Για να μπορέσετε να βρείτε στοίχηματα αξίας, πρέπει πρώτα να μπορείτε να εκτιμήσετε την πραγματική πιθανότητα των αποτελεσμάτων των γεγονότων. Μετά από αυτό, μόλις γνωρίζετε τις αληθινές πιθανότητες, πρέπει να βρείτε την απόδοση που καθιστούν την ανισότητα K * P > 1 αληθής.
Είναι πολύ δύσκολο να προσδιορίσουμε την πραγματική πιθανότητα των αποτελεσμάτων σε γεγονότα όπως ένας ποδοσφαιρικός αγώνας. Οι εταιρείες στοιχημάτων προσλαμβάνουν ολόκληρα τμήματα επαγγελματιών αναλυτών για να προβλέψουν τα αποτελέσματα των αγώνων.
Υπάρχουν δύο κύριες μέθοδοι για την πρόβλεψη των αποτελεσμάτων:
Η πρώτη μέθοδος χρησιμοποιείται ευρέως από τις εταιρείες στοιχημάτων. Προσπαθούν να χρησιμοποιήσουν όλα τα δεδομένα που έχουν για να εκτιμήσουν την πιθανότητα νίκης μιας συγκεκριμένης ομάδας. Υπάρχουν επαγγελματίες παίκτες στοιχημάτων που γνωρίζουν επίσης πολύ καλά τις ομάδες και μπορούν να προβλέψουν τα αποτελέσματα με την ίδια ακρίβεια όπως οι εταιρείες στοιχημάτων. Η αναλυτική μέθοδος, ωστόσο, απαιτεί εκτενή γνώση του αντικειμένου και είναι δύσκολο να αυτοματοποιηθεί.
Η δεύτερη μέθοδος βασίζεται στη στατιστική. Εάν έχετε τις απόδοση από έναν μεγάλο αριθμό εταιρειών στοιχημάτων, μπορείτε να υπολογίσετε το περιθώριο εταιρείας στοιχημάτων κάθε μίας από την απόδοση. Μπορείτε να χρησιμοποιήσετε το περιθώριο για να προσπαθήσετε να προσδιορίσετε πώς ο εταιρεία στοιχημάτων αξιολόγησε την πιθανότητα. Τέλος, υπολογίζετε τη μέση τιμή – και αυτή θα είναι η πιο ακριβής πρόβλεψη, καθώς βασίζεται στη δουλειά πολλών αναλυτών. Αυτή η μέθοδος μπορεί να φαίνεται λιγότερο ακριβής για ορισμένα άτομα, αλλά μπορεί να αυτοματοποιηθεί εύκολα.
Η υπηρεσία μας χρησιμοποιεί τη στατιστική προσέγγιση για να βρει στοιχήματα αξίας.
Μια σίγουρη στοιχηματική πρόταση έχει πάντα μία ενδιαφέρουσα ιδιότητα. Αν υποθέσετε ότι όλα τα πονταρίσματα μιας συγκεκριμένης σίγουρο στοίχημα πρότασης ανήκουν σε μια μόνο εταιρεία στοιχημάτων και υπολογίσετε το περιθώριο, θα πάρετε έναν αρνητικό αριθμό. Ας ελέγξουμε μία από τις σίγουρες στοιχηματικές προτάσεις.
1/2 + 1/3,75 + 1/5 = 0,9667 ( < 1 )
Το περιθώριο ισούται με: (0,9667 - 1) * 100% = -3,33%
Αυτό σημαίνει ότι τουλάχιστον ένα από τα πονταρίσματα στη σίγουρο στοίχημα είναι υπερεκτιμημένο. Δηλαδή, ανάμεσα σε όλα τα πονταρίσματα οποιασδήποτε σίγουρο στοίχημα πρότασης με θετικό κέρδος, υπάρχει τουλάχιστον μία στοίχημα αξίας (αλλά μπορεί να υπάρχουν περισσότερες). Βασικά, αυτή η υπερεκτιμημένη στήριξη έχει πιθανώς προκαλέσει τη σίγουρο στοίχημα και όλες οι άλλες σίγουρο στοίχηματα χρησιμοποιούνται μόνο για να την καλύψουν.
Με αυτόν τον τρόπο, αν έχετε μια λίστα με τις βρεθείσες σίγουρο στοίχηματα για την ίδια εκδήλωση, μπορείτε να προσπαθήσετε να προσδιορίσετε ποιο ποντάρισμα τις έχει προκαλέσει. Για παράδειγμα, αν όλες οι σίγουρο στοίχημα για την ίδια εκδήλωση περιέχουν ένα ποντάρισμα για τη νίκη της πρώτης ομάδας από την ίδια εταιρεία στοιχημάτων, είναι προφανές ότι αυτό το ποντάρισμα είναι υπερεκτιμημένο.
Σε αντίθεση με σίγουρα στοιχήματα, οι στοιχηματισμοί αξίας έχουν τα πλεονεκτήματα και τα μειονεκτήματα τους.
Πλεονεκτήματα
Λιγότερα πονταρίσματα. Όταν χρησιμοποιείτε σίγουρα στοιχήματα, πρέπει να τοποθετήσετε πονταρίσματα σε όλα τα αποτελέσματα των σίγουρων στοιχημάτων, και αν δεν μπορέσετε να τοποθετήσετε τουλάχιστον ένα από αυτά, ρισκάρετε να χάσετε όλα τα άλλα στοιχήματα. Όταν παίζετε με στοιχήματα αξίας, πρέπει να κάνετε ένα ποντάρισμα ανά στοίχημα αξίας, ελαχιστοποιώντας έτσι τον κίνδυνο ότι δεν θα μπορείτε να τοποθετήσετε άλλα πονταρίσματα.
Λιγότεροι λογαριασμοί σε εταιρείες στοιχημάτων. Για να παίξετε με σίγουρα στοιχήματα, χρειάζεστε τουλάχιστον δύο ή τρεις λογαριασμούς σε διαφορετικές εταιρείες (αλλά όσο περισσότερους, τόσο το καλύτερο). Όταν παίζετε με στοιχήματα αξίας, χρειάζεστε μόνο έναν λογαριασμό.
Η συμπεριφορά του παίκτη είναι πιο φυσική. Όταν παίζετε με σίγουρα στοιχήματα, ο παίκτης αναγκάζεται να υπακούει στον υπολογιστή και να τοποθετεί εξαρτημένα πονταρίσματα. Μια εταιρεία στοιχημάτων μπορεί να βρει περίεργο το γεγονός ότι ένας παίκτης ποντάρει πάντα κάτι όπως $5,43 σε σύνολο 13,5 σε αγώνες όπως Γουατεμάλα - Γουαδελούπη. Όταν παίζετε με στοιχήματα αξίας, μπορείτε να ποντάρετε οποιοδήποτε ποσό δεν αναιρεί τη στρατηγική που έχετε επιλέξει. Αυτό προκαλεί λιγότερες υποψίες.
Στη θεωρία, το στοίχημα αξίας είναι πιο κερδοφόρο από το σίγουρο στοίχημα. Δεδομένου ότι κάθε σίγουρο στοίχημα περιλαμβάνει τόσο ένα υπερτιμημένο στοίχημα όσο και εναλλακτικά στοιχήματα, κάθε σίγουρο στοίχημα παίκτης τα τοποθετεί όλα, όχι μόνο εκείνο που μπορεί να είναι κερδοφόρο. Ο παίκτης σχεδόν αγοράζει ασφάλιση κατά των απωλειών, αλλά πρέπει να την αποπληρώσει με σημαντικό κόστος. Αν βρεθούν και χρησιμοποιηθούν αποτελεσματικά οι υπερεκτιμημένες στηρίξεις, ο παίκτης θα κερδίσει περισσότερα χρήματα κατά μέσο όρο, καθώς δεν καταβάλλεται το περιθώριο της εταιρείας στοιχημάτων.
Μειονεκτήματα
